Sheet 06 Gauss Theorem
- Given figure shows three charges \(q_{1}\), \(q_{2}\) and \(q_{3}\) enclosed in gaussian surface. How much is the flux of electric field through Gaussian surface if \(q_{1}=+4nC\), \(q_{2}=-7nC\) and \(q_{3}=+9nC\).

Ans: \(\phi_{E}=\left(6.78\times10^{2}\right)Nm^{2}C^{-1}\). - If, a charge of \(1C\) is placed at the centre of a cube of side \(10cm\), then calculate flux coming out of the any surface of the cube. If, charge is placed at the one vertex of the cube then then calculate: the flux also.
Ans: \(\phi^{‘}_{E}=\frac{1}{6}\phi\) and \(\phi^{”}_{E}=\frac{1}{24}\phi_{E}\). - The electric field components in below figure are \(E_{x}=\alpha x^{\frac{1}{2}}\), \(E_{y}=E_{z}=0\) in which \(\alpha=800\frac{N}{cm^{2}}\). Calculate:
(a) The flux \(\phi_{E}\) through the cube.
(b) The charge enclosed by the cube. Assume that, \(a=0.1m\).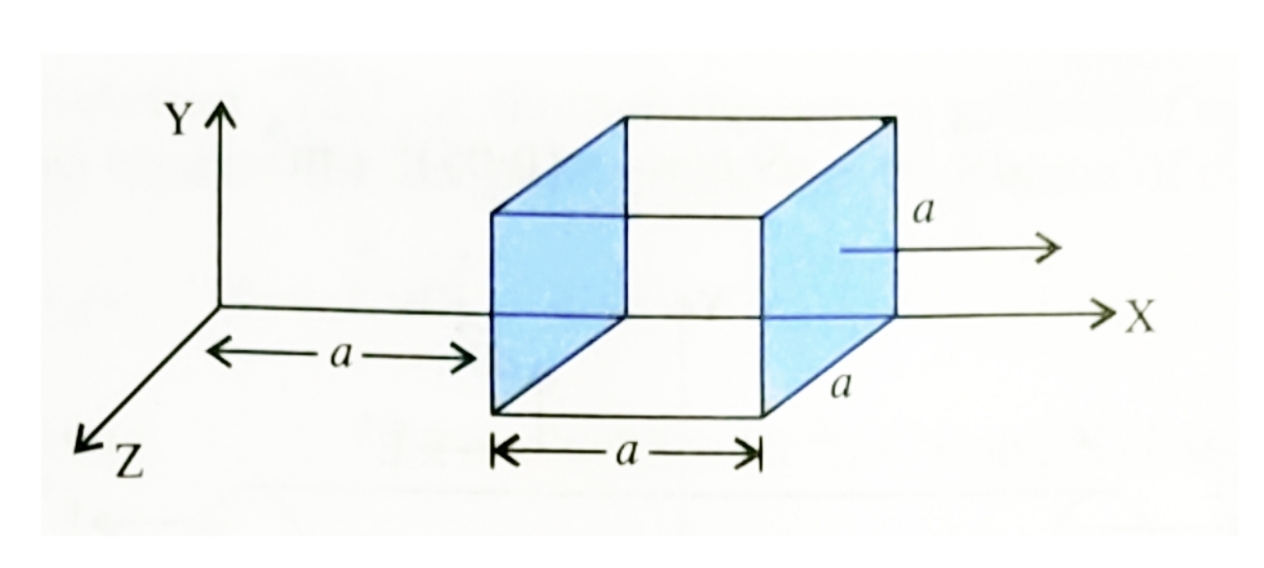
Ans: (a) \(\phi_{E}=1.05Nm^{2}C^{-1}\) and (b) \(q=\left(9.27\times10^{-12}\right)C\). - In given figure, Calculate the total flux through the sphere \(S_{1}\) and \(S_{2}\). The wire AB shown in the figure, has a linear charge density \(\lambda\) given by; \(\lambda=kx\). Where; x is the distance measured along the wire from end A.
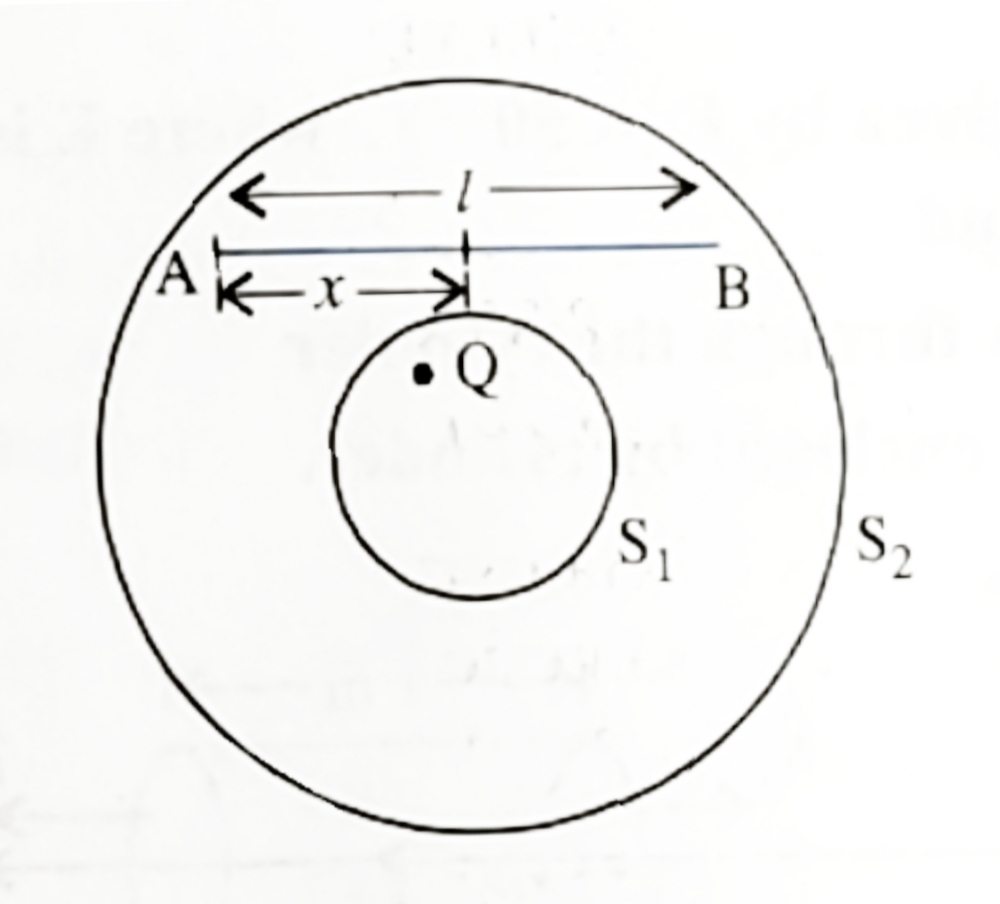
Ans: \(\phi_{1}=\frac{Q}{\epsilon_{o}}\) and \(\phi_{2}=\frac{Q}{\epsilon_{o}}+\frac{kl^{2}}{2\epsilon_{o}}\). - \(S_{1}\) and \(S_{2}\) are two hollow concentric spheres enclosing charges \(Q\) and \(2Q\) respectively as shown in the figure:
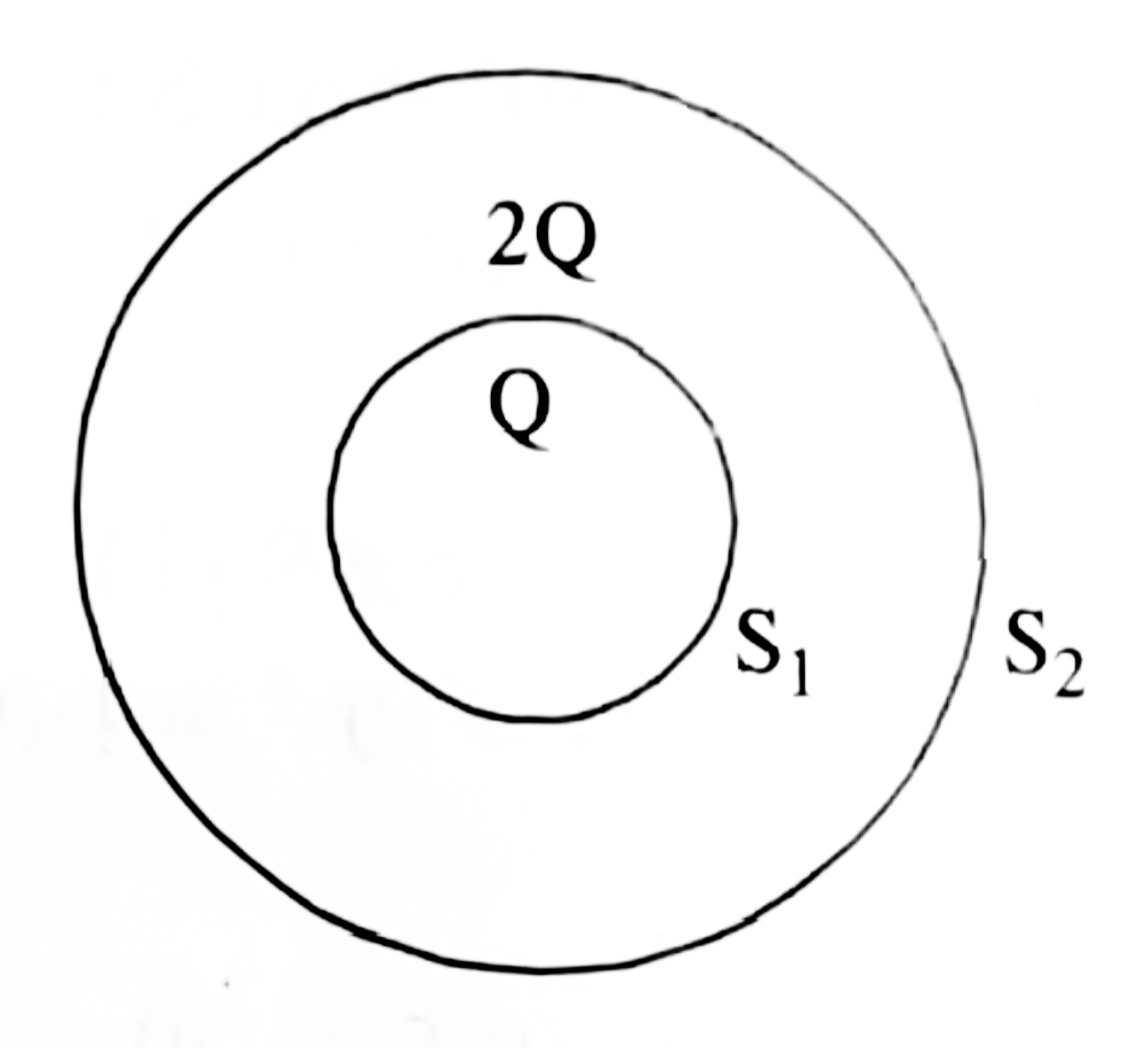
(a) What is the ratio of electric flux through \(S_{1}\) and \(S_{2}\)?
(b) How will the electric flux through the sphere \(S_{1}\) changes if a medium of dielectric constant \(5\) is introduced in the space inside \(S_{1}\) in place of air.
(c) How the electric flux through the sphere \(S_{1}\) changes, if a medium of dielectric constant K is introduced in the space inside \(S_{2}\) in place of air?
Ans: (a) \(\frac{\phi_{1}}{\phi_{2}}=\frac{1}{3}\) (b) \(\phi^{‘}_{2}=\frac{Q}{5\epsilon_{o}}\) and (c) \(Unaltered\). - The electric field components due to a charge inside the cube of side \(0.1m\) are \(E_{x}=\alpha x\), where \(\alpha=500\frac{N}{Cm}\), \(E_{y}=E_{z}=0\). Calculate: the flux through the cube and charge inside the cube.
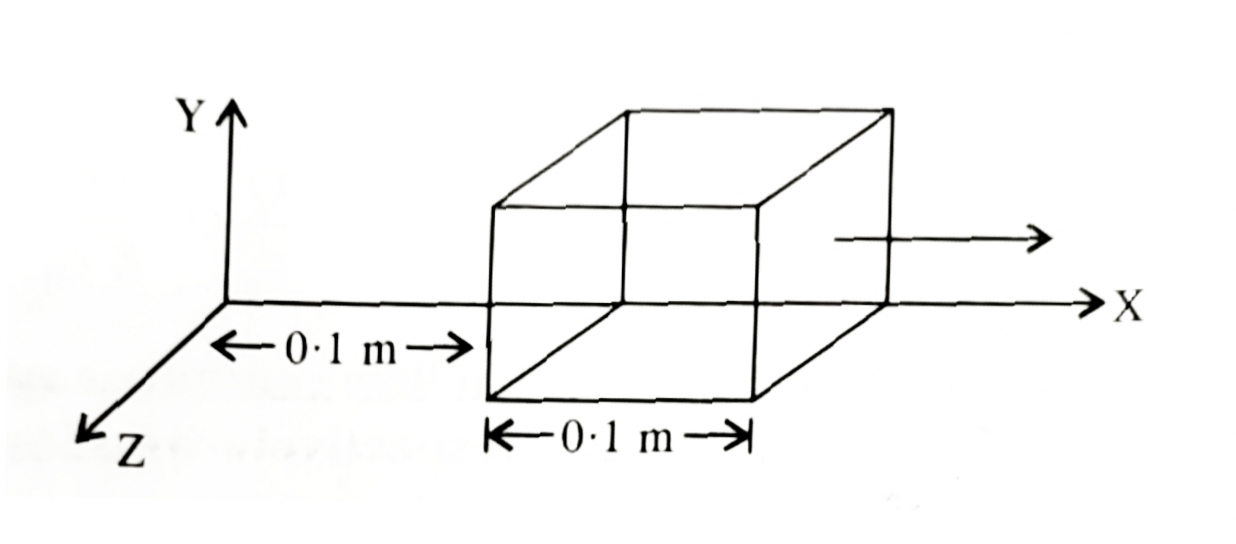
Ans: \(\phi_{E}=0.5\frac{Nm^{2}}{C}\) and \(\left(4.425\times10^{-12}\right)C\). - An electric field is uniform, and in the positive x-direction for positive x and uniform with the same magnitude in the negative x-direction for negative x, It is given that;
\(\vec{E}=200\hat{i}\frac{N}{C}\) for \(x>0\) and
\(\vec{E}=-200\hat{i}\frac{N}{C}\) for \(x<0\).
A right circular cylinder of length \(20cm\) and radius \(5cm\) has its center at the origin and its axis along the x-axis so that one face is \(x=+10cm\) and the other is at \(x=-10cm\).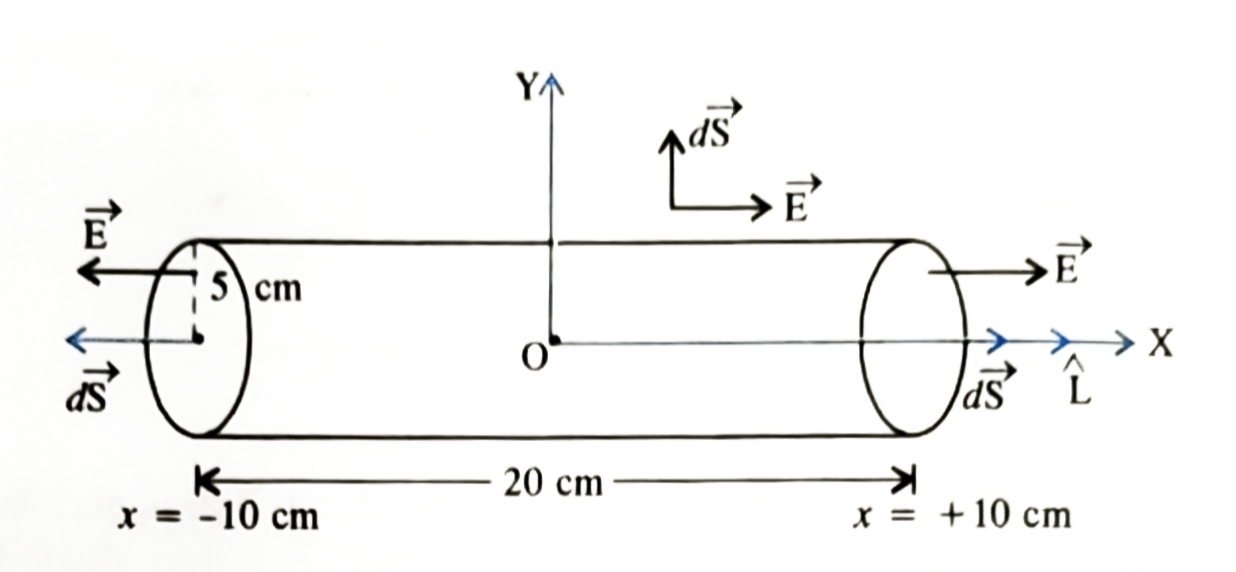
(i) What is the net outward flux through each flat surface?
(ii) What is the flux through the side if the cylinder?
(iii) What is net outward flux through cylinder?
(iv) What is the net charge inside the cylinder?
Ans: (i) \(\phi_{L}=1.57\frac{Nm^{2}}{C}\) (ii) \(\phi_{R}=1.57\frac{Nm^{2}}{C}\) and (iii) \(\phi_{cylinder}=3.14\frac{Nm^{2}}{C}\) and (iv) \(\left(2.78\times10^{-11}\right)C\), - A hollow cylindrical box of length \(1m\) and area of cross-section \(25cm^{2}\) is placed in a three dimensional co-ordinate system as shown in below figure. The electric field in the region is given by \(\vec{E}=50x\hat{i}\frac{N}{C}\), and \(x\) is in metre. Find:
(i) Net flux through the cylinder.
(ii) Charge enclosed by cylinder.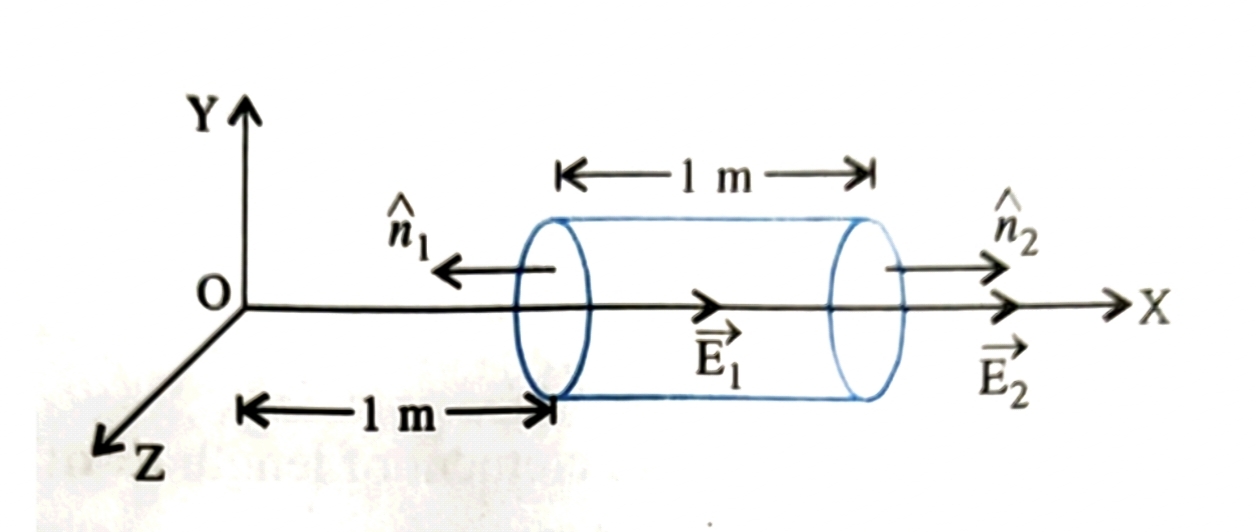
Ans: (i) \(\phi_{NET}=\left(1.250\times10^{-1}\right)\frac{Nm^{2}}{C}\) and (ii) \(q=1.06pF\). - If, the electric field \(\vec{E}=\left(6\hat{i}+3\hat{j}+4\hat{k}\right)\), Calculate: the electric flux through a surface of area \(20Units\) in Y_Z plane.
Ans: \(120Units\). - An uniform electric field \(\vec{E}=E_{x}\hat{i}\frac{N}{C}\) for \(x>0\) and \(\vec{E}=-E_{y}\hat{i}\frac{N}{C}\) for \(x<0\) are given. A right circular cylinder of length \(L\) cm and radius \(r\) cm has its center at the origin and its axis along x-axis. Find: out the net electric flux. Using Gauss’s Theorem write the expression of the net charge with in cylinder.
Ans: \(\left[2\pi r^{2}E_{x}\left(10\right)^{-4}\right]\frac{Nm^{2}}{C}\) and \(\left[2\pi r^{2}\epsilon_{o} E_{x}\left(10\right)^{-4}\right]\frac{Nm^{2}}{C}\).