Current Electricity (12Acd04)

Sheet 03 Combinations of Resistance.

1. Two coils have a combined resistance of \(9\Omega\) when connected in series and \(2\Omega\) when connected in parallel. Find: The resistance of each coil.
   
   Ans: \(R_{1}=6\Omega\) and \(R_{2}=3\Omega\).
   
   
2. Two resistances are in the ratio of \(1:4\). If, these are connected in parallel, their total resistance becomes \(20\Omega\). Find: Value of each resistance?
   
   Ans: \(R_{1}=25\Omega\) and \(R_{2}=100\Omega\).
   
   
3. A parallel combination of these resistances takes a current of \(75 A\) from a \(30V\) battery. If, the two resistances are \(10\Omega\) and \(12\Omega\), Find: their third resistance.
   
   Ans: \(R_{3}=15\Omega\).
   
   
4. A wire of resistance \(4R\) is bent in the form of a circle as shown in figure. What is the effective resistance between the ends of the diameter?
   
   
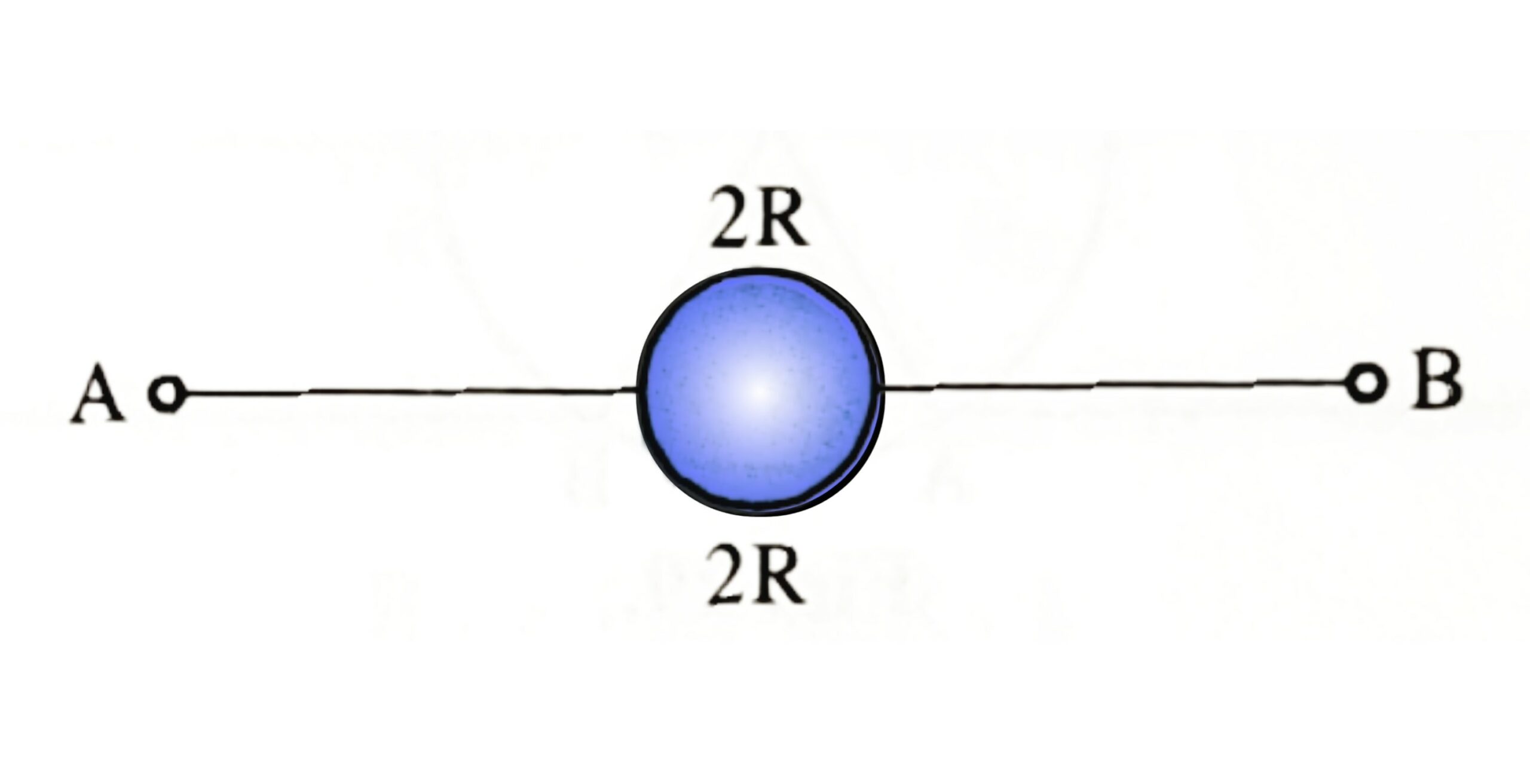
   Ans: \(R_{equ}=R\).
   
   
5. A resistor of \(24\Omega\) resistance is bent in the form of a circle as shown in below figure. What is the equivalent resistance between points A and B.
   
   
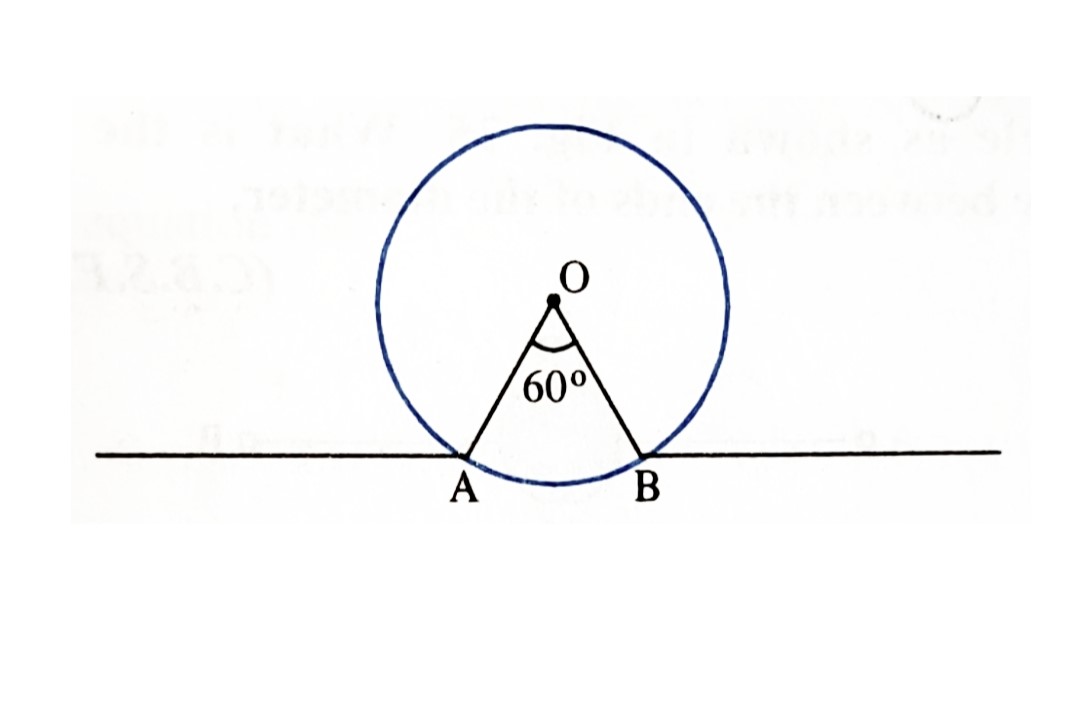
   Ans: \(R_{equ}=3.33\Omega\).
   
   
6. What is the equivalent resistance between points A and B in following circuit.
   
   
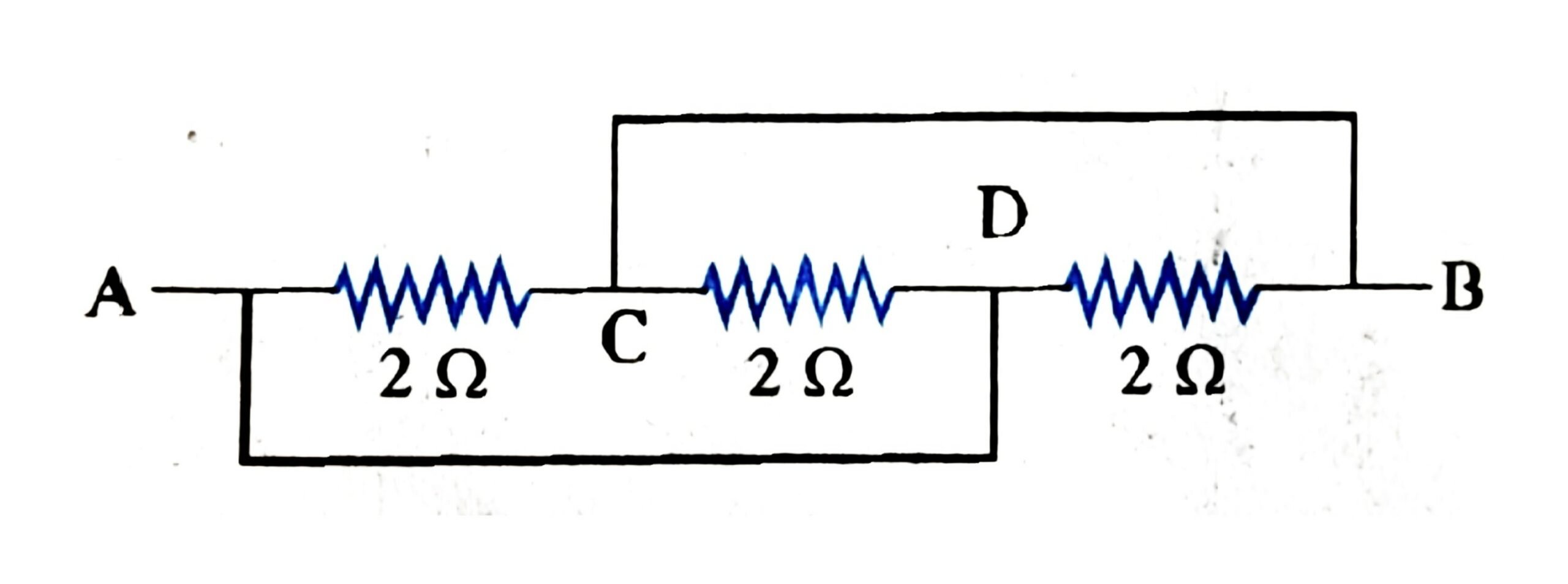
   Ans: \(R_{equ}=0.67\omega\).
   
   
7. Two resistances of conductance \(G_{1}\) and \(G_{2}\) are connected in series. They are connected to another conductor of conductance \(G_{3}\). Determine: their equivalent conductance.
   
   Ans: \(G_{equ}=\frac{\left(G_{1}.G_{2}+G_{2}.G_{3}+G_{3}.G_{4}\right)}{\left(G_{1}+G_{2}\right)}\).
   
   
8. Two rods of copper and aluminium each having length \(20 cm\) and equal cross-section area \(2mm^{2}\) are joined (i)In series. and (ii) In parallel as shown in figures. Find: The resistance of the combination in each case. Given: the resistivity of copper, \(\rho_{Cu}=\left(1.7\times10^{-8}\right) \Omega m\) and resistivity of aluminium, \(\rho_{Al}=\left(26\times10^{-8}\right) \Omega m\).
   
   
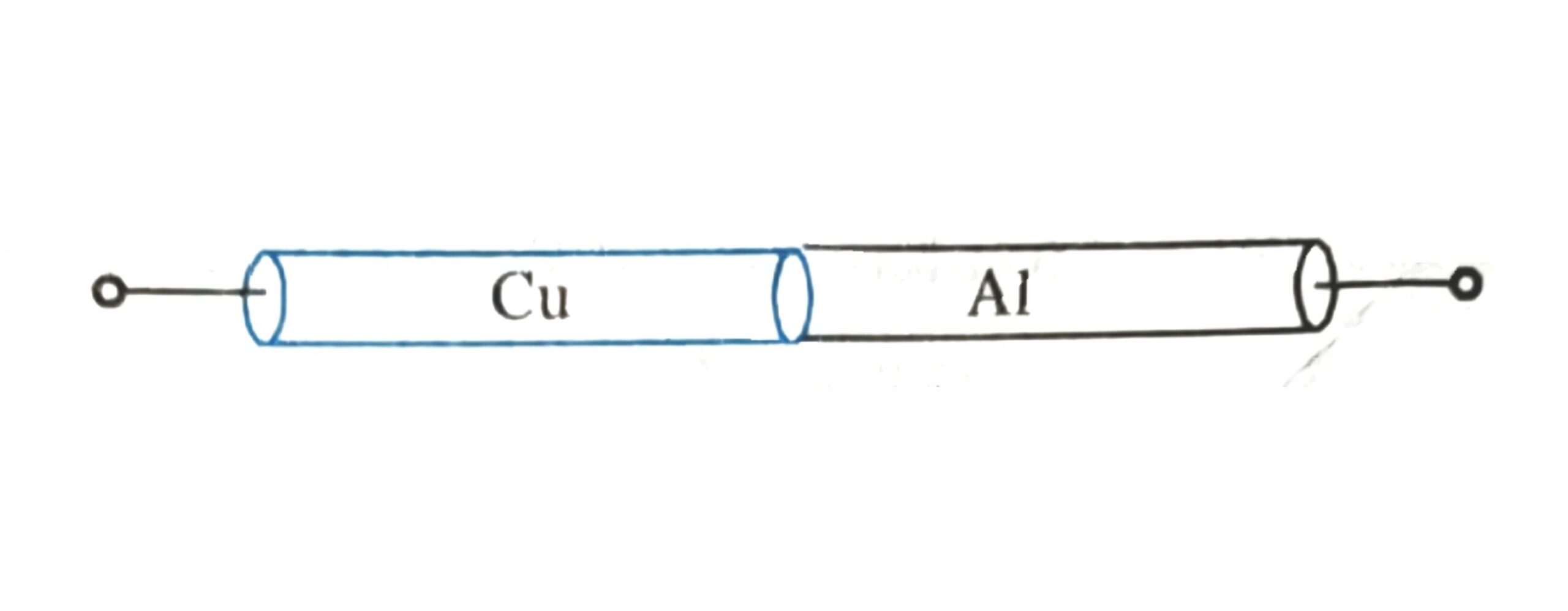
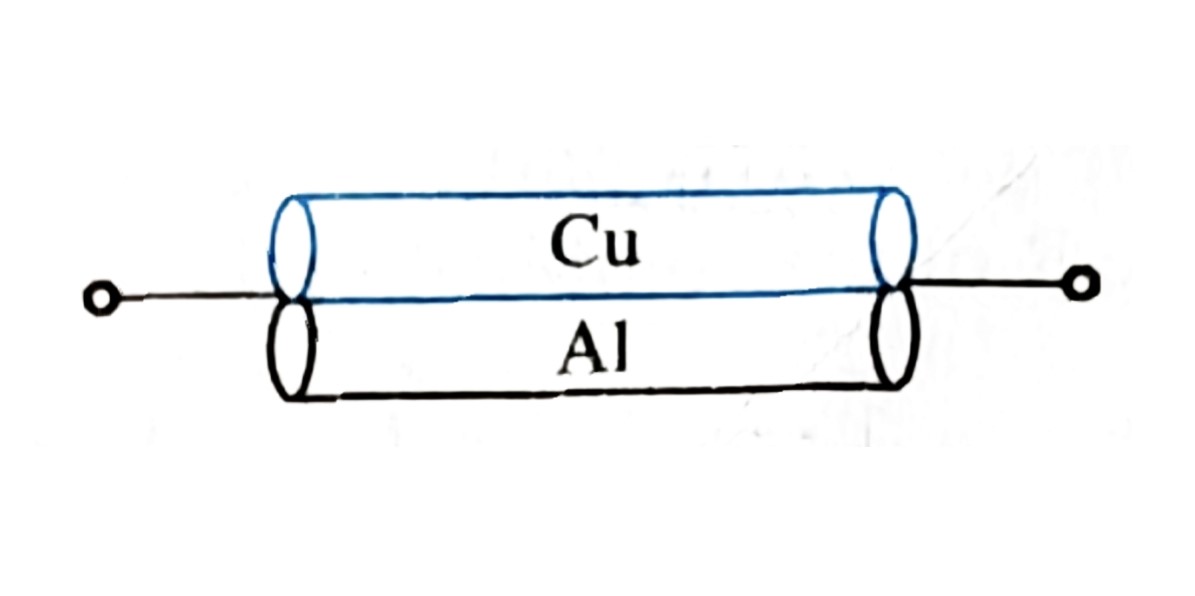
   Ans: \(R_{series}=\left(4.3\times 10^{-3}\right)\Omega\) and \(R_{parallel}=\left(1.028\times 10^{-3}\right)\Omega\).
   
   
9. In the given network of resistors, find the equivalent resistance (i) Between the points A and B. (ii) Between points A and D. (iii) Between the points A and C.
   
   
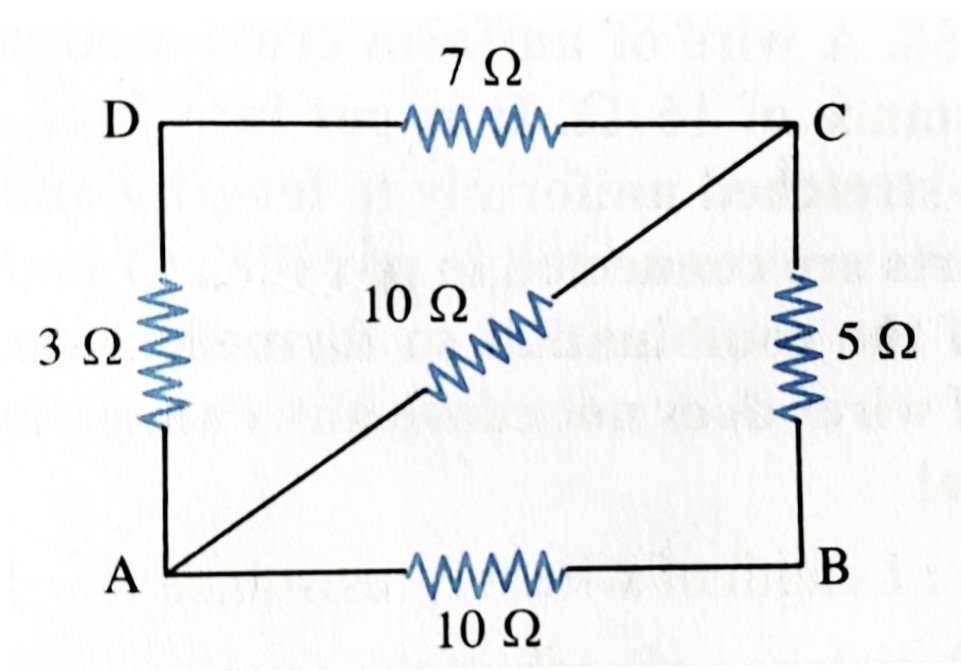
   Ans: \(R_{AB}=5\Omega\), \(R_{AD}=\frac{39}{16}\Omega\) and \(R_{AC}=\frac{15}{4}\).
   
   
10. Calculate: The current through the ammeter A in given circuit.
    
    
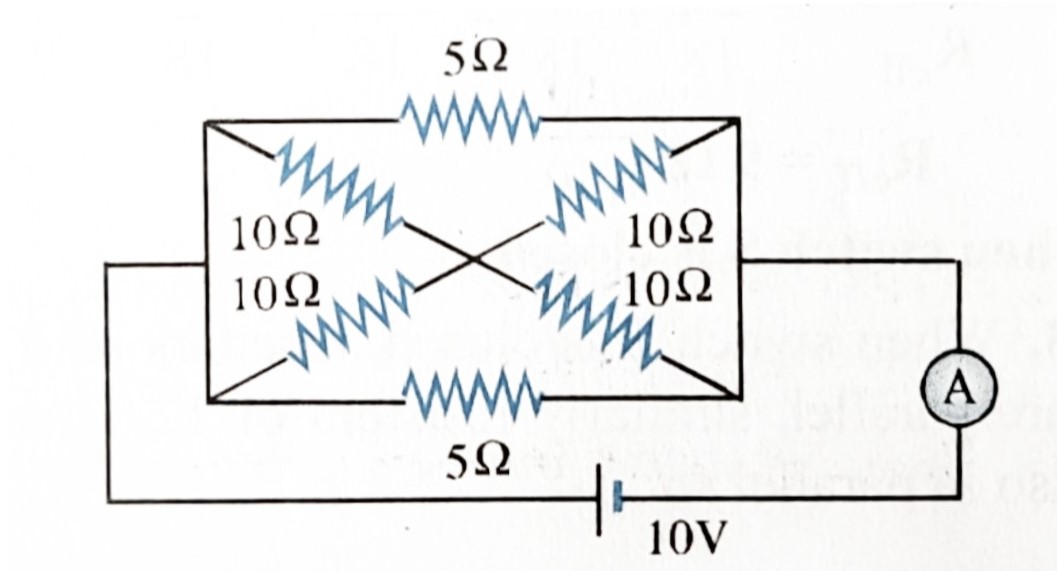
    Ans: \(I=5A\).